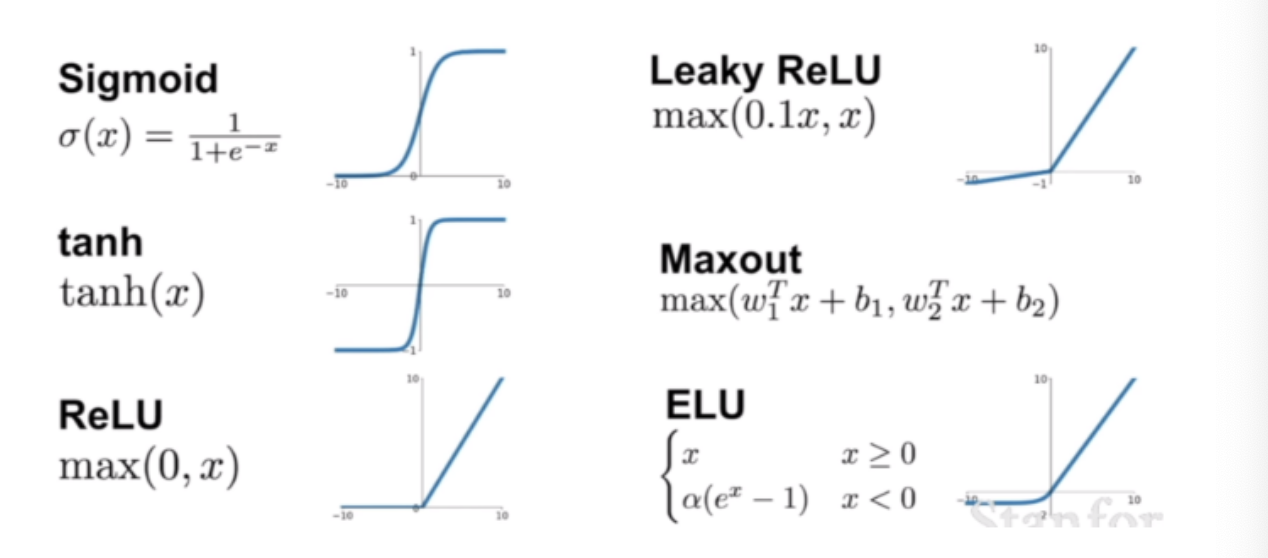
3.activation function

활성화 함수 종류 및 비교

활성화 함수란?

• 활성화 함수는 딥러닝 네트워크에서 노드에 입려된 값들을 비선형 함수를 통해 다음 레이어로 전달하는데 이때 사용되는 함수를 활성화 함수(Activation Function) 이라고 한다.
• 왜? 사용할까?
  • 활성화 함수를 사용하는 이유는 선형함수인 h(x)=cx를 사용하게 되면
    • 3층 네트워크의 경우, y(x)=h(h(h(x)))= c x c x c x x 가 된다.
  • 따라서 은닉층이 없는 네트워크가 된다.
  • 뉴럴네트워크에서 층을 쌓는 혜택을 얻고 싶으면 활성화함수를 반드시 비선형 함수를 사용해야 한다.
• 활성화 함수의 역할
  • 인공신경망에서 활성화 함수는 입력데이터를 다음 레이어에서 어떻게 출력되는지의 역할을 한다. 즉, 활성화 함수는 입력을 받아서 활성화 또는 비활성화를 결정하는데 사용되는 함수

활성화 함수의 종류

1. sigmoid 함수

• Logistic 함수 (0~1사이의 값을 가지므로)

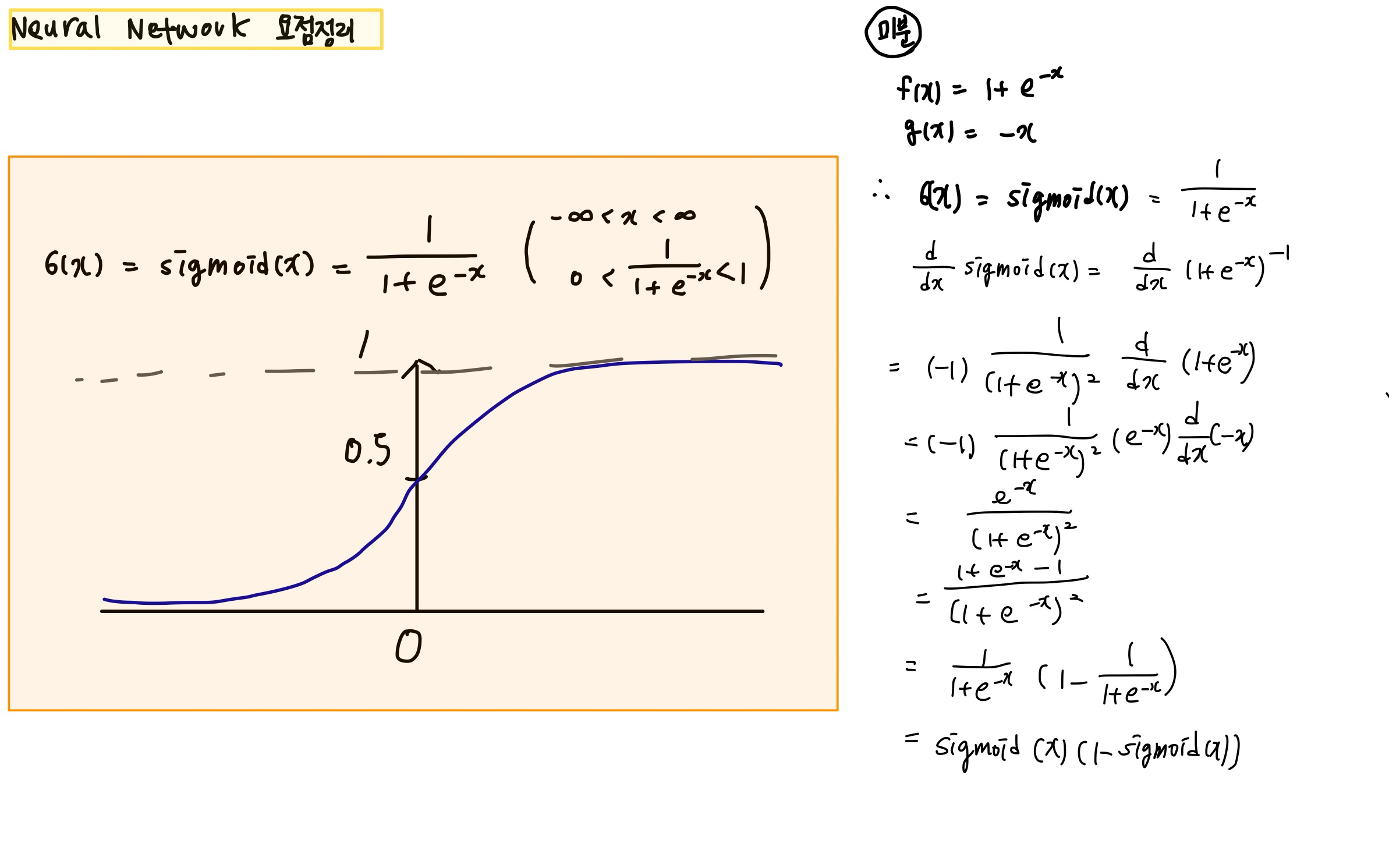
• 장점
  • 모든 실수 값이 0보다 크고 1보다 작아서 Logistic Classification, 비용함수(Cost funcion)에 많이 사용
  • sigmoid()의 리턴 값이 확률 값이기 때문에 확률로 해석할 때 용이
• 단점
  • sigmoid 함수는 음수 갑승ㄹ 0 에 가깝게 표현하기 때문에 입력값이 최종 레이어에서 미치는 영향이 적어지는 vanishing gradient problem이 발생
  • 또한, sigmoid 도함수 그래프에서 미분 계수는 최대값이 0.25이다.
  • Back-propagationd을 계산하면서 활성화 함수의 미분값을 곱하는 과정이 포함되는데, sigmoid함수의 경우 은닉층의 깊이가 깊으면 오차율이 계산하기 힘듦(Vanishing Gradient Problem)
  • 즉, x의 절대값이 커질수록 Gradient Backpropagation 시 미분값 이 소실될 가능성이 큼
  • sigmoid 함수의 중심이 0 이여서 합습이 느려질 수 있음

2. Tanh 함수

Hyperbolic Tangent Function 은 쌍곡선 함수 중 하나 (sigmoid 함수의 변형)

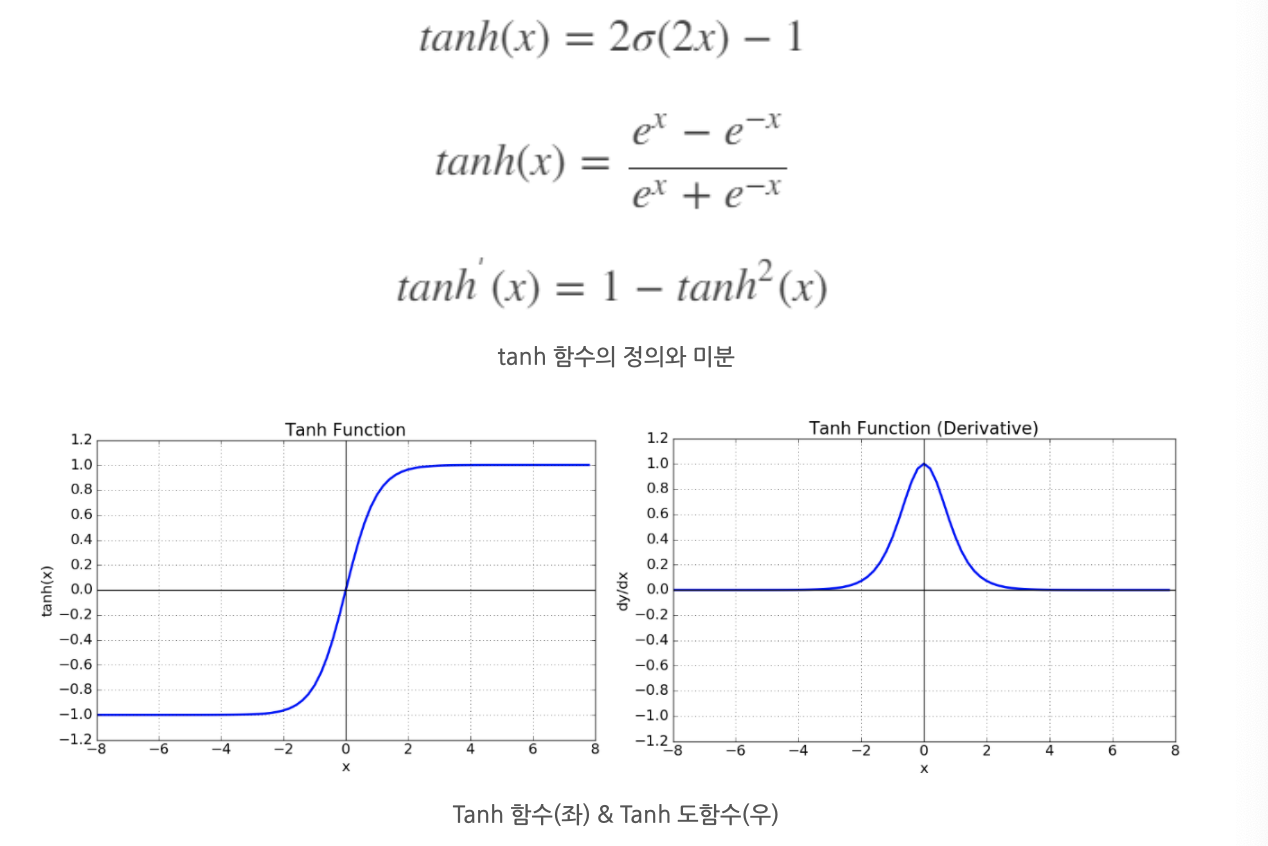
• 장점 단점
  • sigmoid 의 최적화 과정에서 중심을 0으로 옮김으로서 최적화의 속도를 높임
  • 단점 : Vanishing Gradient Problem은 여전히 남아있음

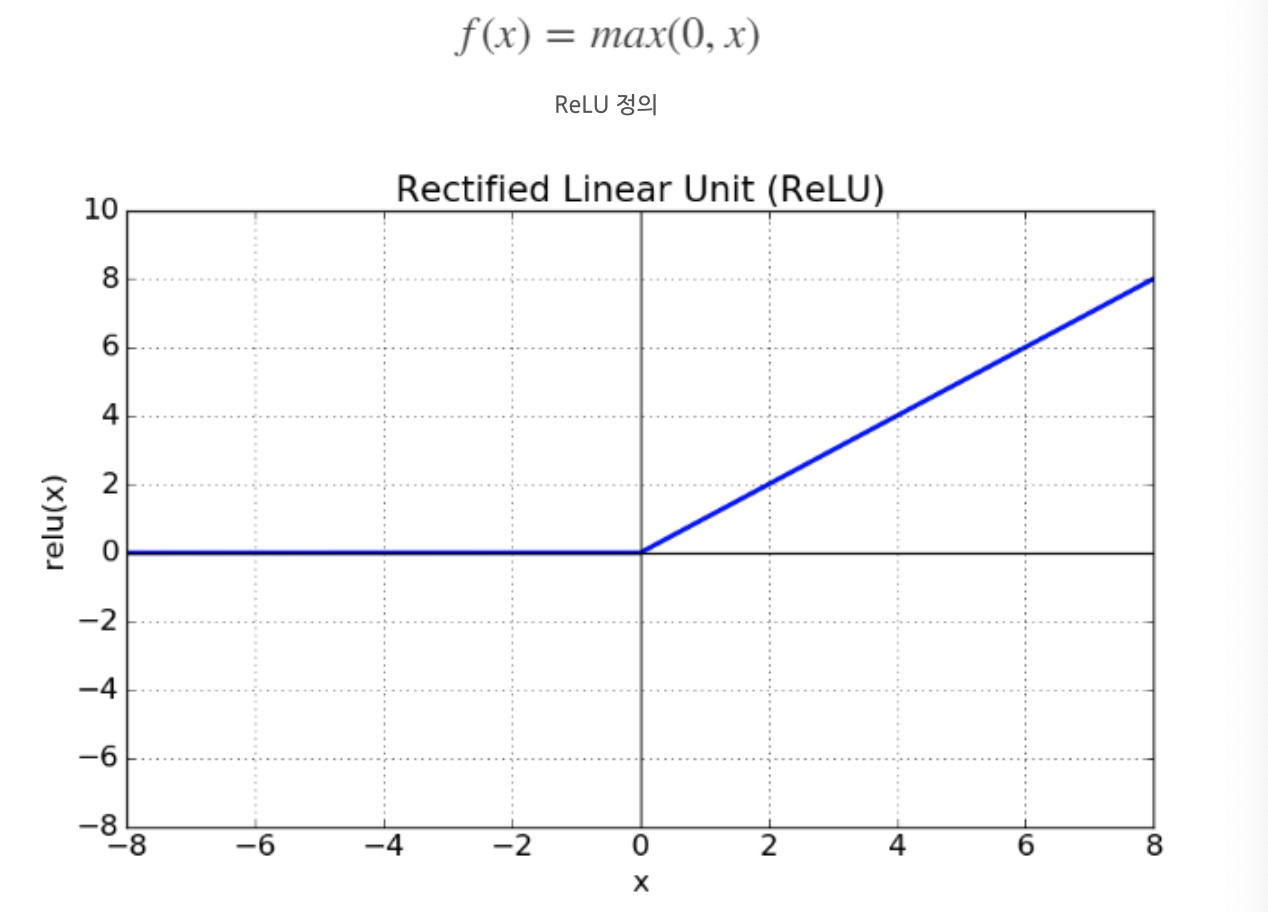
3. ReLU

ReLU(Rectified Linear Unit, 경사함수)는 가장 많이 사용되는 활성화 함수 중 하나

Gradient Vanishing 문제를 해결하는 함수

4. Leaky ReLU

dying relu을 해결하기 위한 함수

5. PReLU

Leaky ReLU와 거의 유사한 파라미터 (알파)를 추가해 xrㅏ 음수인 영역에서도 기울기를 학습

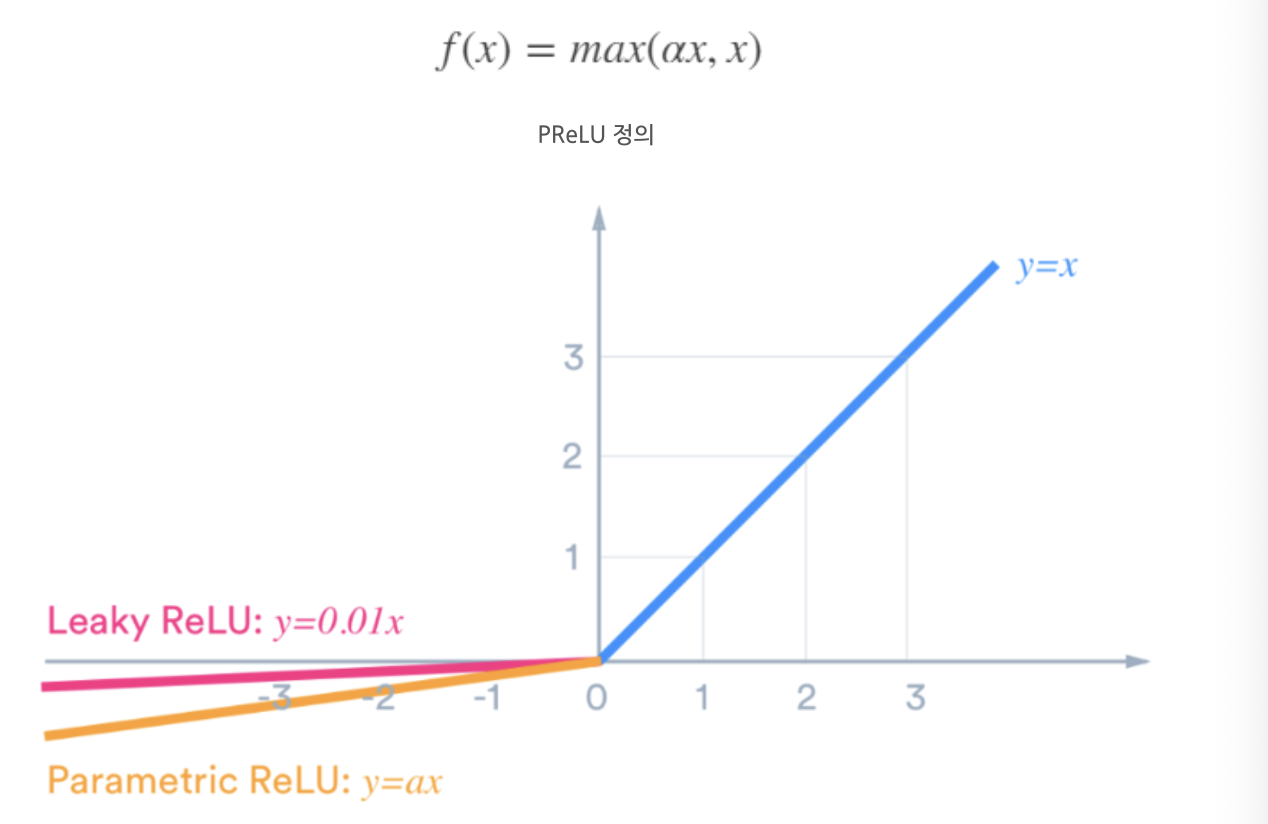
비교